Dot Products

The dot product is also known as the Euclidean inner product. It is an operation between two vectors that returns a scalar result. It can be represented in a couple of ways. Given two vectors, $v$ and $w$, and the angle between them as $\theta$, the dot product is: $$v \cdot w=||v||||w||\cos\theta$$

$||v||$ is the norm of $v$ and is a measure of distance. For a 3D vector, it is calculated as: $$||v|| = \sqrt{x^2 + y^2 + z^2}$$

You can also calculate the dot product without $\theta$ with this equation: $$v \cdot w=v_x w_x + v_y w_y + v_z w_z$$

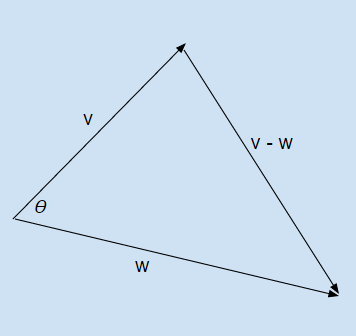
The Law of Cosines is what enables this equivalency. When talking about two vectors, imagine placing them end to end with $\theta$ as the angle between the vectors. If you were to form a triangle, the side opposite of $\theta$ would be the vector $v - w$.

The Law of Cosines gives us this equation: $$||v-w||^2 = ||v||^2 + ||w||^2 - 2||v|| ||w|| \cos\theta$$

After plugging in the equations for the length of each side ($\sqrt{x^2 + y^2 + z^2}$) and reducing terms, you will arrive at: $$||v|| ||w||\cos\theta = v_x w_x + v_y w_y + v_z w_z$$

So, $v \cdot w=||v||||w||\cos\theta=v_x w_x + v_y w_y + v_z w_z$.

What is the dot product useful for? It can tell you about the angle between two vectors which is useful in line of sight tests.

• If $v$ and $w$ are perpendicular, the dot product will be 0.
• If $v \cdot w < 0$, $\theta$ is greater than $90^{\circ}$ and a target is behind the observer
• If $v \cdot w > 0$, $\theta$ is less than $90^{\circ}$ and a target is in front of the observer

Further Reading

Van Verth, James M., Lars M. Bishop. "Vectors and Points." Essential Mathematics for Games and Interactive Applications. 3rd ed. Boca Raton: CRC, 2016. Web. ISBN 978-1482250923.

-- Chris Edwards (Senior Engine Programmer)